DassFlow 1D & 2D

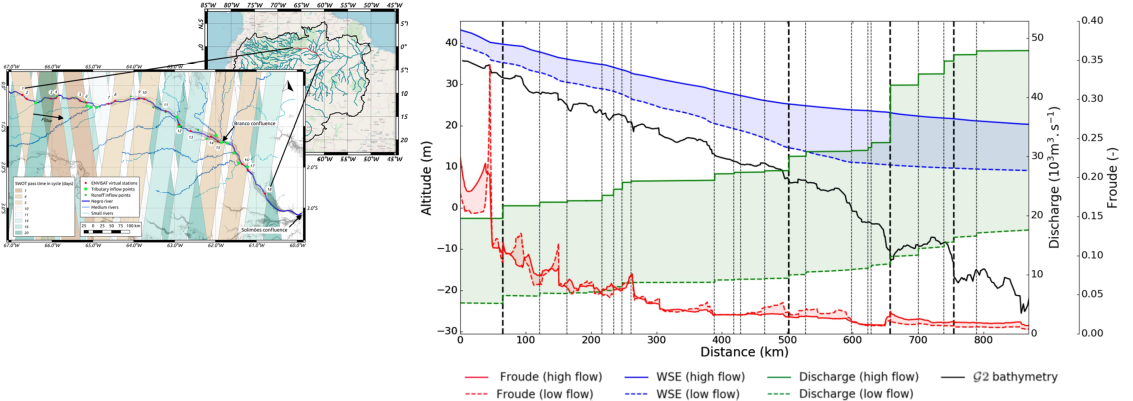
1D hydraulic model

Fine scale 1D hydraulic model with hydrological inflows of the Negro River in the Amazon basin built from multi-satellite and in situ data. From [Pujol et al. 2020, JoH]

What is DassFlow ?

DassFlow (Data Assimilation for Free Surface Flows) denotes a set of computational codes aiming at modeling free surface geophysical flows with data assimilation capabilities. These flows can be water-rivers flows (Newtonian rheology) but also ice-glaciers flows (power-laws rheology) or lavas, muds flows1 etc (based on Herschel-Bulskley rheology laws). The dynamics flow models rely, mainly but not only, on the Shallow Water systems (depth-integrated equations, long-wave assumption).

Two code versions are available:
DassFlow1D : networks of 1D river flow models.
DassFlow2D : accurate and robust 2D flows with wet-dry front dynamics; affordable over river networks with a 1D-like 2D approach (see Fig.); spatialized modeling of hydrological source terms and boundary conditions.

The basic technologies of both codes are described in the Shared technologies for all codes page.

DassFlow1D

What does it include ?

  • The 1D Shallow Water system (Saint-Venant’s equations) in variables (S,Q)(x,t).
  • The Diffusive Wave equation (the standard one and an original two-scales one).
  • Multi-branches (rivers network).
  • Data Assimilation capabilities (variational or not) from multi-source / multi-nature data.
  • The numerical schemes are: the classical Preissmann FD scheme or potentially FV schemes.
  • Documentations, benchmarks (analytical, toys, real data).
  • Global Sensitivity Analyses / UQ are quite easy to implement by interfacing with e.g. OpenTurns library.
  • An additional original flow model dedicated to spatial hydrology is available: a low-Froude algebraic model.

Key applications

  • 1D river flows, potentially network.
  • “Effective cross-sections” inference.
  • Assimilation of multi-source data.
  • Spatial hydrology: see the HiVDI algorithm , which enables to estimate rivers discharge at global scale from SWOT measurements.

Test cases and real-world applications of HiVDI (based on DassFlow1D)

DassFlow2D

What does it include ?

  • The 2D Shallow Water system in variables (h,qx,qy) solved by accurate FV schemes (1st order or actual 2nd order). Robust treatment of wet-dry front dynamics.
  • A capability to locally degenerate the 2D model into a 1D-like model (therefore much less CPU-time consuming). This enables to build up e.g. multiple branches 1D-like models with 2D zooms at the branches junction, or in highest-interest areas, or in inundations areas.
  • Various Boundary Conditions enable to tackle real-world problems.
  • The GR4 hydrological model (developed by L. Santos and G. Thirel from INRAe, HYCAR Research Unit) is a lumped hydrological model implemented in a semi-distributed manner in DassFLow2D. This enables to perform hydrological calibration via hydraulic information feedback in a sequential coupling GR4 - Shallow Water 2D.
    To consider a fully distributed hydrological model, please use SMASH .
  • The corresponding adjoint code and a complete 4D-var optimization process (see the Shared technologies page).
  • Parallel computations (MPI Fortran).
  • Assimilation of multi-source data.
  • Documentations.
  • Benchmarks (analytical, toys, real data cases).
  • An easy use of Python libraries such as deep learning, signal processing and statistics libraries since the Fortran computational kernel code is wrapped in Python (see the Shared technologies page).
  • A Reduced Order Model (ROMs) of DassFlow2D is in progress.

Key applications

  • Rivers network dynamics with local zooms, e.g. in inundation areas (integrated 1D-2D flow solvers).
  • Flood plain dynamics with wet-dry fronts.
  • Lava / mud flows (Herschel-Bulckley rheology).

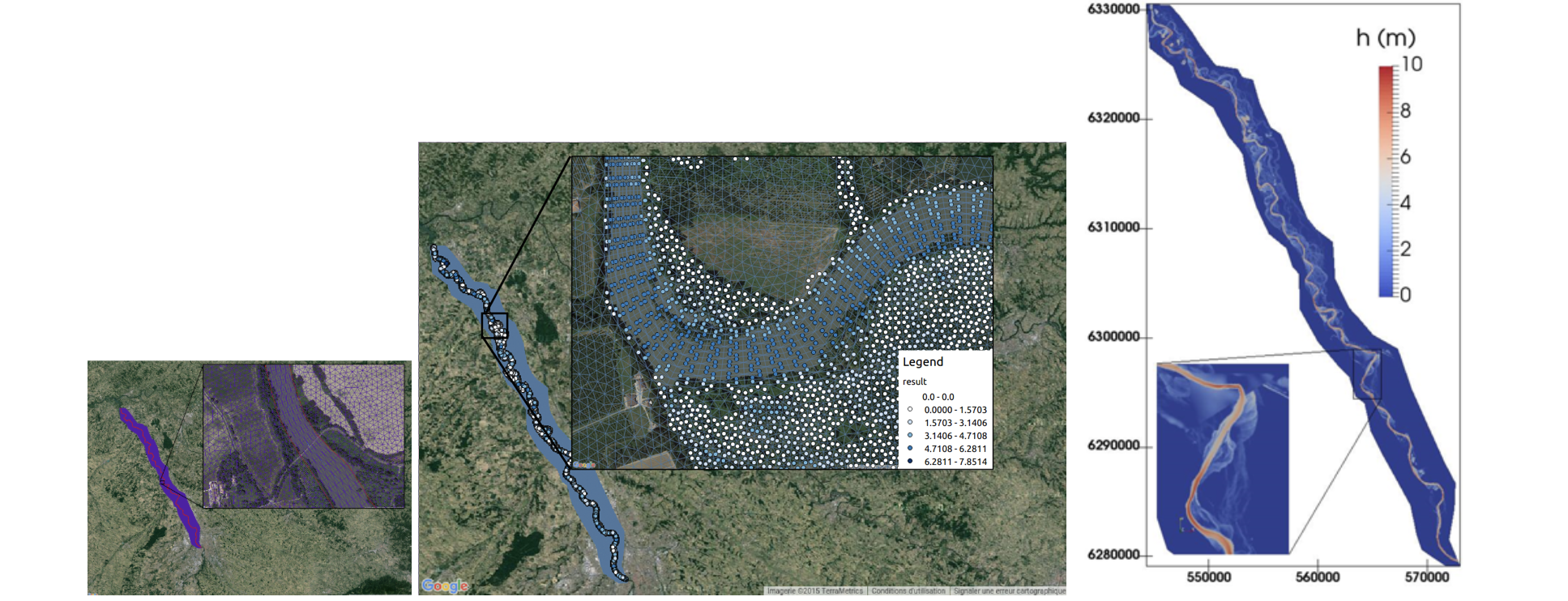
Garonne_river

Full 2D computations of Garonne river (Toulouse-Castelsarrasin portion, southern France). 87O K cells (MPI computations both for the direct and the adjoint codes). Datasets provided by D. Dartus et al. IMFT, regional flood forecasting center (SPC Toulouse). Solver from [J. Monnier, F. Couderc, D. Dartus, K. Larnier, R. Madec, J.P. Vila. “Inverse algorithms for 2D shallow water equations in presence of wet dry fronts. Application to flood plain dynamics”. AWR 2016.]

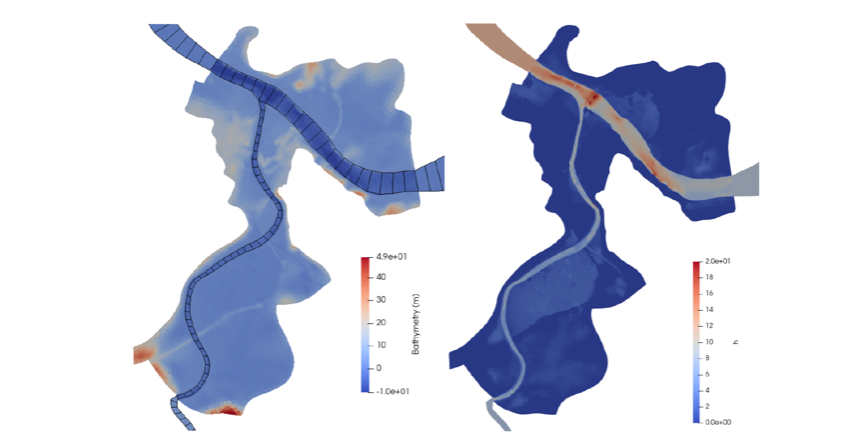
Bayonne_zoom

Mixed 1D-like / 2D computations of the Adour river southwestern France. Datasets provided by the regional flood forecasting center (SPC GAD). Image from [Pujol-Garambois-Monnier, GMD 2022].

Test cases and real-world applications of DassFlow2D

Greetings to the great former contributors of DassFlow!

Other versions

  • DassFlow-RheoPy: DassFlow-RheoPy denotes purely Python codes for various shallow flows models: multi-regimes non-Newtonian fluids (power-law, Bingham, Herschel-Bulkley rheologies).
    • One-equation models (lubrication type).
    • Two-equation models (Shallow-Water type).
    • Plug type model (SSA in glaciology).
    • Finite Elements schemes (FEniCS library).
    • Continuous adjoint equations.

Applications: Glaciers dynamics (e.g. in ice-sheets), volcano lavas.

For examples in glaciology:
J. Monnier, J. Zhu. “Physically-constrained data-driven inversions to infer the bed topography beneath glaciers flows. Application to East Antarctica”. Computational Geosciences, vol. 25, pp 1793-1819, 2021. DOI
  • DassFlow-3d: Stokes like systems-power law rheology, low inertia, FE schemes.

DassFlow is developed under the GNU AFFERO GENERAL PUBLIC LICENSE.
For more information, please contact the PIs.

s Some references for DassFlow are available on this page.

  1. These features are yet to be implemented in future releases of DassFlow. ↩︎